Todo operador de opciones sabe que las letras griegas son herramientas fundamentales a la hora de gestionar el riesgo de nuestras posiciones y cartera.
Las letras griegas más conocidas, y que ya hemos hablado de ellas en anteriores artículos, son Delta, Vega, Theta y Gamma.
Esas letras son las más utilizadas y las que la mayoría de las plataformas de análisis de riesgos nos muestran.
Sin embargo, existen otras muchas letras griegas, de segundo y tercer orden, algunas muy útiles para operar.
De las principales letras griegas debes saber que Delta, Vega y Theta son de primer orden, es decir, nos miden la sensibilidad del precio de una acción con respecto a un parámetro determinado (precio, tiempo o volatilidad).
También existe Rho, de primer orden, pero como depende de la variación de los tipos de interés, y estos no se mueven a diario, tiene poca importancia.
Gamma, aunque también se utiliza mucho, es una griega de segundo orden, ya que mide el ratio de cambio de delta con respecto al precio.
Quizá estés sorprendido de que has estado utilizando durante mucho tiempo una griega de segundo orden, como gamma, sin saberlo.
Y también es muy probable que hayas estado utilizando conceptos prácticos a la hora de operar, definidos por griegas de segundo orden, también sin saberlo.
Por ello, la idea de este artículo es dar un poco de claridad, y sobre todo de practicidad, en lo a las letras de segundo orden se refiere.
Tipos de Letras Griegas de Segundo Orden
Ya sabemos que las griegas de segundo orden nos miden los cambios de las letras de primer orden (Delta, Vega, Theta) con respecto a una variable determinada, que siempre va a ser el precio, el tiempo o la volatilidad.
Hay en total 6 tipos de griegas de segundo orden, pero no todas tienen gran utilidad práctica:
Gamma: mide el ratio de cambio de Delta con respecto al precio
Vomma: mide el ratio de cambio de Vega con respecto a la volatilidad
Vanna: mide el ratio de cambio de Delta con respecto a la volatilidad
Charm: mide el ratio de cambio de Delta con respecto al paso del tiempo
Vera: mide el ratio de cambio de Rho con respecto a la volatilidad
Veta: mide el ratio de cambio de Vega con respecto al tiempo
Y luego tenemos más griegas de tercer orden como Speed, Zomma, Color y Ultima pero que no hablaré de ellas de momento.
De las griegas de segundo orden, las más importantes son Gamma, Vomma, Vanna y Charm.
Como Gamma es la más conocida, voy a enfocarme en las otras tres. Vamos a ver de forma gráfica lo que esas griegas nos dicen y cómo nos pueden ayudar a la hora de operar, especialmente en técnicas de coberturas.
Charm
Ya hemos visto que Charm nos mide el ratio de cambio de Delta con respecto al paso del tiempo.
Y te puedes preguntar, ¿y para qué quiero saber yo eso?
Es simple. Si tienes una estrategia con opciones, es bueno que sepas cómo tu línea de beneficio va a ir evolucionando con el tiempo. Y eso es precisamente lo que Charm te mide.
Una forma sencilla de verlo es en una plataforma de gráficos de riesgo, donde puedes configurar las líneas de beneficios en diferentes escalones, por ejemplo cada 7 días desde el día de hoy.
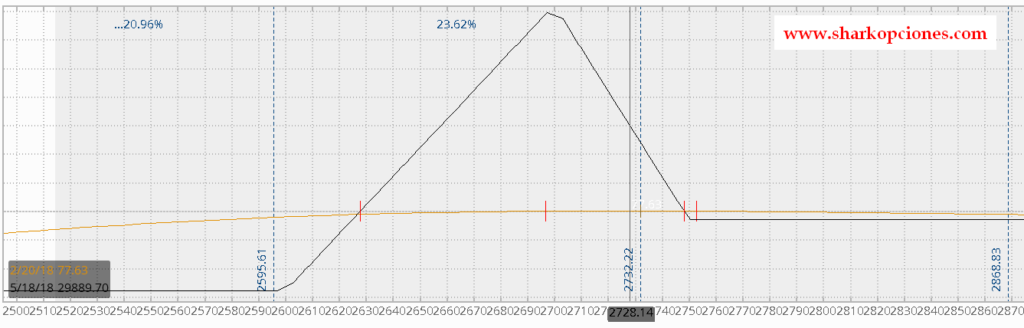
Por ejemplo, en la siguiente imagen podemos observar un gráfico de riesgo que nos muestra una estrategia específica. Vemos en línea amarilla lo que sería la evolución del beneficio/pérdida en el día actual y en línea negra en el momento de expiración:
Si sobre esa estrategia queremos ver cómo evoluciona delta con el paso del tiempo, es decir, Charm, es tan fácil como configurar por ejemplo la evolución de la línea amarilla cada 20 días, que es lo que se observa en la siguiente gráfica.
Cada línea de un color nos representa la evolución de los beneficios/pérdidas en diferentes estados temporales (cada 20 días), y en cada línea podemos observar cómo Delta evolucionaría según se mueva el precio.
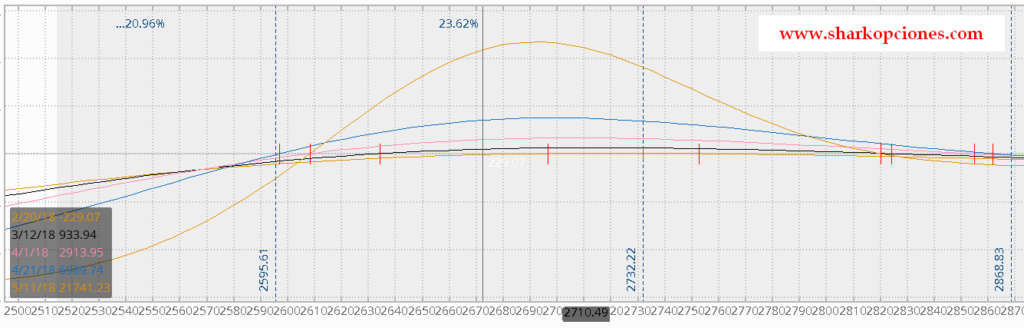
Esto sería un ejemplo práctico de cómo estamos utilizando la griega de segundo orden Charm en nuestra operativa.
Vanna
Vanna mide el ratio de cambio de Delta con respecto a la volatilidad.
Si hacemos un ejercicio similar que el anterior, sobre la estrategia ejemplo, en el siguiente gráfico podemos ver cómo variaría el delta de nuestra posición según se incremente la volatilidad.
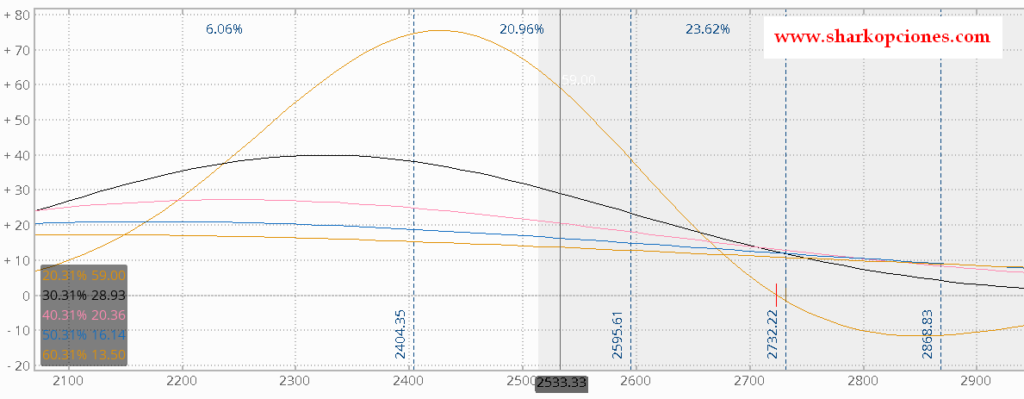
Sabemos de nuestro gráfico inicial, que el delta de la posición se hace cada vez más negativo desde los 2700 hacia abajo.
Vanna, lo que nos está diciendo, es que ese delta negativo se va a hacer mucho más grande con el primer salto de volatilidad del 10%. Luego, con los sucesivos saltos de 10 puntos, el cambio de ratio es menor.
Esto no sería bueno para mi estrategia, pues si el precio cae, mi delta negativo se va a hacer cada vez más negativo con el incremento de volatilidad, lo que se traduce en mayores pérdidas.
Vomma
Y por último Vomma, que nos mide el ratio de cambio de Vega con respecto a la volatilidad.
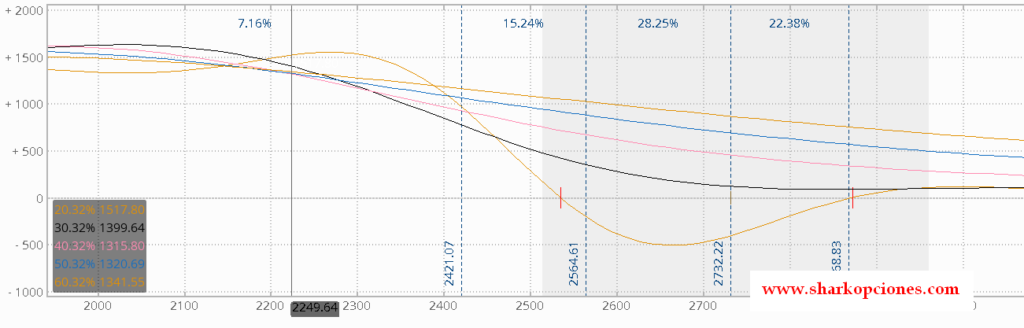
Igualmente, si observamos sobre nuestra estrategia inicial cómo varía Vega al subir la volatilidad en diferentes saltos del 10%, obtenemos lo siguiente:
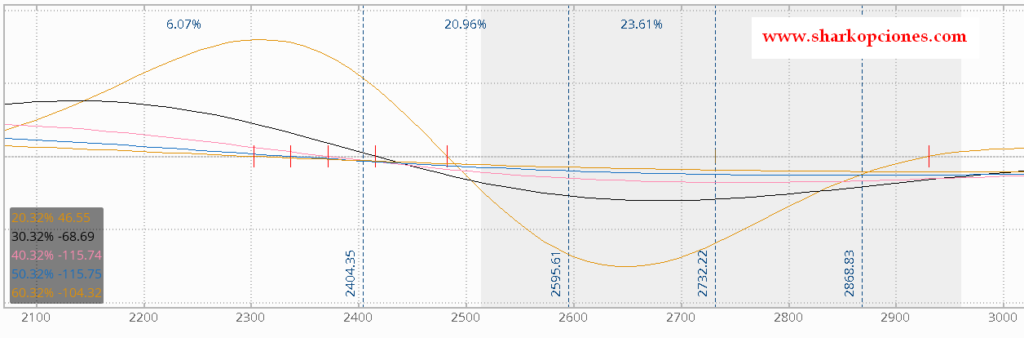
Observamos que por debajo del strike corto de nuestra estrategia ejemplo, 2700, el ratio de cambio de Vega comienza a aumentar a medida que la volatilidad sube. Luego, con los sucesivos saltos del 10% de volatilidad, el ratio de cambio va siendo menor.
Igualmente, es algo negativo, pues nuestra estrategia inicial es vega negativa, lo que significa que en caídas con incremento de volatilidad, mi estrategia va a perder, y va a perder más a medida que siga aumentando la volatilidad.
Y ahora preguntarás, ¿pero cómo puedo extrapolar todo esto a mi operativa real?
Esta información es muy útil a la hora de analizar y buscar soluciones de cobertura.
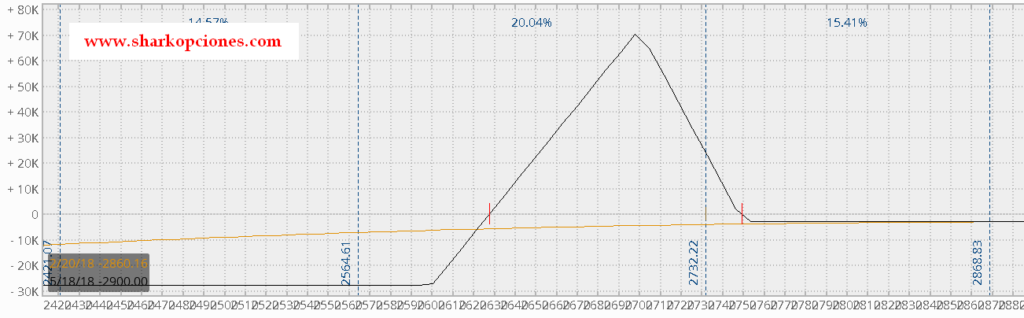
Si sobre nuestra estrategia inicial hacemos una simulación de subida de 10 puntos de volatilidad, lo cual iría acompañado de una brusca caída del precio, observamos que las pérdidas de la posición aumentarían de forma exponencial, precisamente por sus valores de Vomma y Vanna, como acabamos de ver anteriormente.
Esto se ve en el siguiente gráfico. Se observa que la línea amarilla se va hundiendo cada vez más a medida que el precio cae (y caería más la línea si subimos aún más la volatilidad):
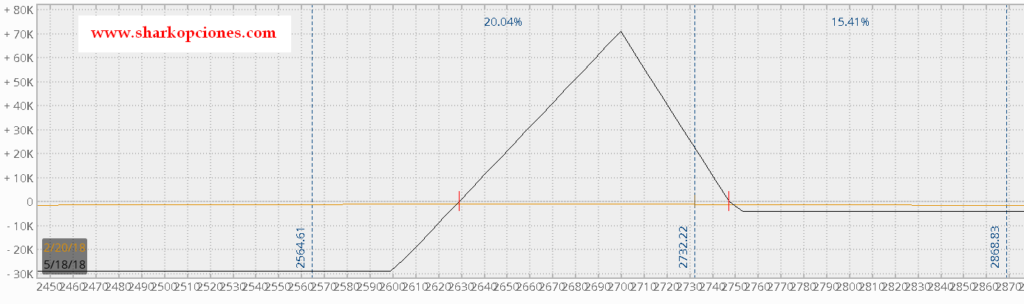
Fíjate en el siguiente gráfico cómo cambia la línea de beneficio cuando le aplicamos una estrategia de cobertura y hacemos la misma simulación de subida de volatilidad.
Se observa que la línea queda aplanada en toda la bajada del precio, lo que se traduce en pérdidas controladas (incluso posibilidad de beneficio si el incremento de IV es mayor).
¿Y cómo quedaría Vanna y Vomma con la estrategia cubierta?
Si analizamos Vanna, vemos en la siguiente imagen que ésta se hace positiva en el primer y segundo “spikes” del 10%, lo cual nos interesa siempre que busquemos coberturas.
Pero también observamos que si el incremento de IV es mayor, la cobertura que tenemos sería insuficiente (esto se ve en los siguientes saltos de IV donde Vanna se torna negativa).
Es decir, si queremos una mayor protección ante un posible crash del 40% en volatilidad, necesitaríamos incrementar nuestras coberturas.
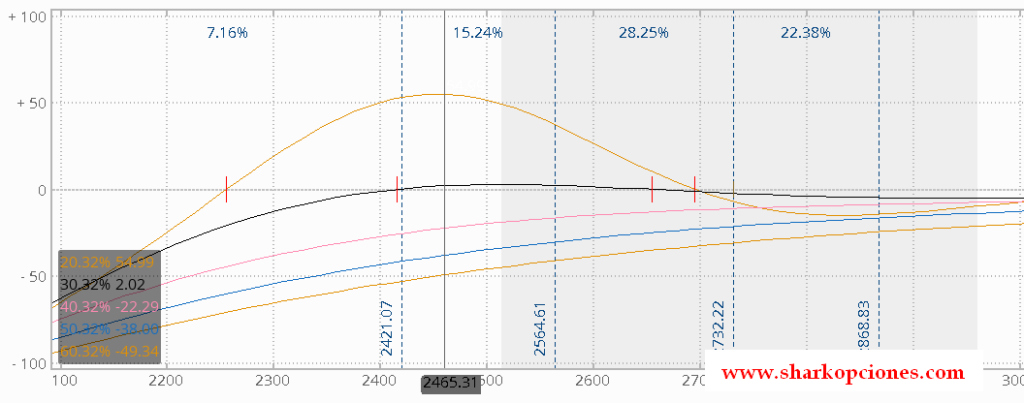
Y si hacemos lo mismo con Vomma, observamos que ésta se torna positiva ante cualquier incremento de volatilidad, que es precisamente lo que buscamos.
En resumen, conocer Vomma, Vanna y Charma en nuestra estrategia nos ayuda a tener una visión más clara de cómo puede comportarse ante los diferentes cambios de mercado, ya sea con el paso del tiempo, movimientos del precio o cambios de volatilidad.
Espero que esta introducción a las griegas de segundo orden te haya sido de interés y te sirva como punto de partida a la hora de configurar tus coberturas.
Saludos y éxitos!!