En la entrega nº 1 tratamos de los elementos de valoración que componen el precio de la prima de una opción y de cómo la volatilidad es la principal dificultad a la hora de operar con este instrumento.
En la entrega nº 2 nos metimos directamente con las engorrosas definiciones de volatilidad, y principalmente tratamos de cómo estimar, de una manera rápida, la volatilidad implícita no de una opción en concreto, que la podemos obtener directamente de la cadena de opciones, sino del subyacente o activo con el que estamos operando. Y vimos que esta estimación tenía una gran importancia ya que puede “adivinar” el rango futuro del precio. Con adivinar y futuro, seguro que te está sonando a bola de cristal. No me extraña, no es para menos, pero… ¿y si fuera verdad?, vamos a verlo.
Lo primero que vamos a hacer es transformar el rango anual que obtuvimos la semana pasada a otro rango más propio de trading:
¿Cómo paso de un rango anual a otro rango?
Modificar la estimación del rango es sencillo. Lo único que es necesario saber es que el rango (la volatilidad) no es proporcional al tiempo sino a la raíz cuadrada del tiempo.
A través de la fórmula que aparece en la siguiente imagen, podemos despejar la volatilidad mensual (de un mes) a partir de la volatilidad anual y de la raíz cuadrada del número de periodos mensuales que contiene una año.
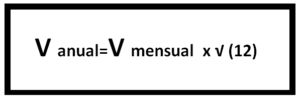
Si quisiéramos obtener la estimación futura de la volatilidad diaria, habría que sustituir Vmensual por Vdiaria y el número 12 por 365. Si quisiéramos obtener el rango semanal sustituiríamos Vmensual por Vsemanal y el número 12 por 52.
Como ejemplo, vamos a calcular el rango estimado para los siguientes dos meses. Por tanto, de la fórmula anterior en la que ya tenemos la Vanual (13.28%), es necesario cambiar el número 12 por 6. Haciendo los cálculos, transformamos un rango anual de 13.28% en un rango para los siguientes 2 meses de 5.52%.
Este valor porcentual, si lo pasamos a valores de precio del SP500, obtenemos 1571.68 como límite inferior y 1755.32 como límite superior (5.52% a ambos lados del precio 1663.5 que es la cotización que hemos tomado como referencia y ejemplo).
¿Qué grado de precisión tienen esto cálculos?
Estos cálculos tienen como premisa previa que la distribución de las cotizaciones deben tener una distribución normal, y realmente no tienen una distribución normal, pero se aproximan mucho. Una distribución normal o distribución de Gauss es un concepto probabilístico que debe cumplir una serie de condiciones. Las distribuciones de precios no son distribuciones normales, pero se pueden aproximar a ellas sin incurrir en demasiados errores.
Si de una serie de datos distribuidos normalmente obtenemos su promedio y su desviación estándar (volatilidad), tendremos una medida de su dispersión.
Según la siguiente imagen, si los precios tuvieran una distribución normal podríamos afirmar, que con una probabilidad del 68.2% (34.1% a cada lado de la media, o precio de referencia) de los casos, los precios se moverían dentro de una desviación estándar, y con una probabilidad del 95.4% (34.1% + 13.6% a cada lado de la media) se moverían dentro de dos desviaciones estándar.
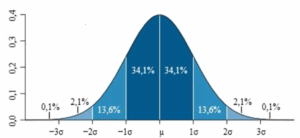
El procedimiento habitual en un cálculo estadístico es tomar unos datos y calcular su media y su desviación estándar para así tener una medida de distribución de esos datos. Sería fácil tomar una serie de cotizaciones de una acción o de un índice y obtener cuál ha sido su media y su desviación estándar (volatilidad histórica). Pero no se trata de eso; queremos saber si las volatilidades implícitas tienen propiedades “adivinatorias” del movimiento futuro de los precios.
¿Se cumplirá esta característica de las distribuciones normales aplicadas al precio y a su desviación estándar, pero empleando la volatilidad implícita?
La respuesta es que sí, y además con una gran precisión.
Si analizamos los movimientos diarios del SP500 durante todo el año 2012, junto con su volatilidad implícita a una semana y vemos el movimiento posterior a esa semana, nos podremos dar cuenta de su capacidad de predicción.
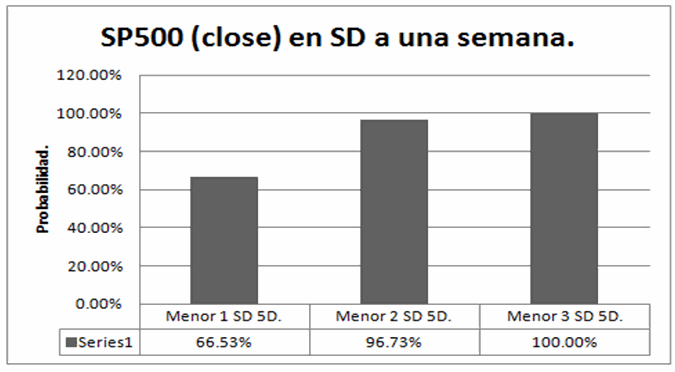
Como se puede observar en la imagen anterior, en la siguiente semana el SP500 se movió dentro de una desviación estándar en el 66.53% de los casos (lo esperado era un 68.2%) y dentro de dos desviaciones estándar en el 96.73% de los casos (lo esperado era un 95.4%). Si el estudio lo repitiéramos para otros periodos de tiempo, diferentes a una semana, los resultados que se obtienen son similares.
Se puede concluir que la volatilidad implícita es una excelente manera de predecir el rango futuro de los precios.
Y para la semana que viene, lo más interesante….Volatilidad IV y terminamos.
SwingTrader